

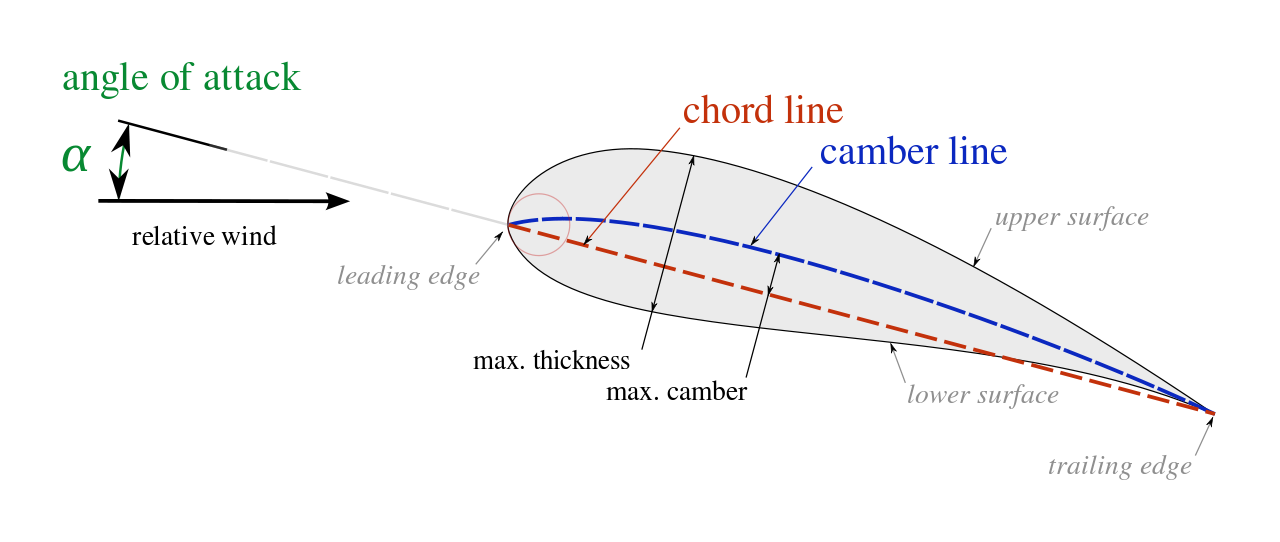
Constructive methods like Shape Function Transformations and PARSEC and deformation methods like Hicks-Henne bump functions and hierarchical Bezier surfaces are described briefly and discussed with reference to their desirable properties of an ideal parameterization scheme. some of the current geometry parameterization schemes with particular reference to their robustness, consistency and their ability to model wide range of shapes within the design space. The interactive link between the geometry modeler and the optimizer is crucial to the successful evolving of the optimal design. The essential components of this optimal shape design process are a geometry modeler, appropriate mesh creator and flow solver and the optimizer. The objective of the optimization is to find the airfoil that enables a maximum lift-over-drag ratio for a target lift coefficient of 0.6. As airfoil design became more sophisticated, this basic approach was modified to include additional variables. In the aircraft industry, shape optimization is fast becoming a major component of aerodynamic design. The shape is adapted by radial basis functions mesh morphing using four parameters (angle of attack, thickness, camber and maximum camber position).
Also new shapes can be produced easily from Bezier curves just by moving the control points, hence Bezier curves can be used to parameterize aerodynamic shapes for shape optimization problems. The results for both the airfoil problems show that sixth-order Bezier curves can model airfoil shapes accurately. Two different airfoil geometries were modeled using Bezier curves in this paper. An iterative process with an initial guess of vector \( t \) was used to find the best possible control points vector \( P \) and vector \( t \). In order to represent an airfoil using Bezier curves we have to find control points vector \( P \) and vector \( t \) of nodes, where each node corresponds to one data point. Its probably not the best airfoil choice for a high performance thermal sailplane. A symmetrical airfoil would be fine for an acrobatic glider designed for slope soaring. These shapes are accurate and smooth enough for direct numerical control (CNC) cutting either 2D section cutting or 5-axis 3D shape milling. Then other factors begin to come into consideration. We observe that sixth-order Bezier can accurately model the airfoil shape. Its the purpose of the model - its mission - that begins the process. In this paper, we have studied Bezier curve approximation of airfoil using fourth-order, sixth-order and eighth-order Bezier curves. The parameterization method used for optimization must be able to accurately model the aerodynamic body and also it should be flexible enough to take all the possible shapes in the design space. Shape parameterization plays an important role in aerodynamic shape optimization process.


 0 kommentar(er)
0 kommentar(er)
